由安徽工业大学公司治理与运营学术论坛主办的第3期学术论坛于2011年4月11日15:30在东区A楼502室召开。
本次学术论坛很荣幸地邀请到了安徽工业大学管理科学与工程学院副教授、硕士生导师陈荣虎博士,陈博士向我们报告了他近期的科研成果《政策分析建模与社会核算矩阵更新》,本次论坛由章铁生博士主持。

陈荣虎博士的报告引起了管工、经济、管理、文法等相关学科老师、学生的广泛关注,顾远、刘家树、崔立志、曾祥飞、沈维成、梅艳晓、季小明、张红侠等老师以及部分研究生参加了讨论。
陈博士首先在演讲中介绍了社会科学中的演化计算工具的演变,产生于上世纪40年代的元胞自动机、产生于上世纪50年代末的系统动力学、可计算一般均衡、上世纪80年代正式出现的演化经济学、上世纪末期出现的现代优化计算算法、复杂自适应系统以及复杂网络等。
陈博士对可计算一般均衡工具进行了介绍,指出第一个可计算一般均衡模型(CGE)模型是1960年Johansen建立的,研究挪威经济增长的多部门增长模型,并介绍了CGE模型的应用领域和CGE模型的结构。

随后陈博士对社会核算矩阵(SAM) 在可计算一般均衡模型(CGE)中起着重要的作用进行了详细分析:由Stone提出的RAS方法(Richard Stone, 1961, Richard Stone and Alan Brown, 1962, 范金、万兴, 2007)由于其简单易行,具有较大的吸引力。但RAS方法的缺点是它不能处理账户(即矩阵)中的负值。为此,学者们提出了不少基于RAS的改进算法,其中,Junius和Oosterhaven(2003)在广义熵的基础上提出了泛化的RAS算法—GRAS算法(以下简称为GRAS-JO算法),GRAS-JO算法能处理账户中的负值,计算过程相对于一些优化方法仍然比较简单,因而仍具有较大的吸引力。万兴等人(万兴等, 2007)对十种社会核算矩阵平衡方法进行比较后得出结论,GRAS-JO算法在众多的算法中排名第2,仅次于交叉熵法。一些学者也指出,GRAS-JO算法并不总是给出最佳结果(Randall W. Jackson and Alan T. Murray, 2004, Michael L. Lahr and Louis de Mesnard, 2004)。Lenzen 等(2007)指出,GRAS-JO算法有个致命的缺点,即在使用原始社会核算矩阵的行和与列和求解新的矩阵时,GRAS-JO算法得出的解偏离了原矩阵,而理想的矩阵应当是原矩阵。为此,Lenzen 等人提出修改GRAS-JO算法,修改后的算法简称为GRAS-LWG算法。尽管GRAS-JO算法和GRAS-LWG算法的结果都在自身的目标函数下是最优的,但在平方距离指标下它们又不是最优的。

在GRAS算法的基础上,保留其基本算法,同时尽量保证计算出的新矩阵与原矩阵间的距离最短,提出改进算法AGRAS。主要思想如下:
GRAS-JO算法的思想是求如公式(1)所示的最小广义熵。
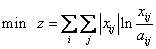 (1)
(1)
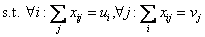
其中aij为原矩阵,xij为欲求的新矩阵,ui、vj分别为对应的行约束(行和)与列约束(列和)。
Lenzen等人将目标函数更改为:
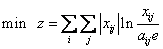 (2)
(2)
AGRAS算法通过进一步改进目标函数,并通过修改相应的算法来获得比GRAS-LWG更优的结果。新的目标函数如公式(3)所示。
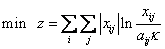 (3)
(3)
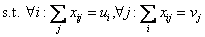
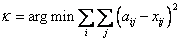
陈博士对AGARS算法进行了详细分析和论证,其可行性和可靠性得到充分保证,从最后的实验结果可以看出,该算法明显优于前人算法。
在陈博士结束对其研究的详细阐述之后,老师和同学们积极参与,纷纷提出自己的想法和问题,得到陈博士及时解答。
最后,章铁生博士对本次论坛做了总结。章博士对陈博士来本论坛参加学术交流表示感谢,对陈博士的研究报告给予高度肯定。
为促进经济管理等相关学科发展,提高年轻教师和研究生的科研水平,扩大学术交流与合作,安徽工业大学公司治理与运营学术论坛将继续邀请校内外著名学者前来举行学术论坛,下一期论坛正在筹办中。
(撰稿:公司治理与运营研究中心)
附录:学术论坛部分问答
Q:公式(3)中κ的取值是否有一个范围?取值太大或太小是否影响其收敛?
A:κ的取值是随机选取,不一定要给其设定范围,因为参数的确定过程是一个迭代过程,通过看迭代是否收敛来确定参数的值;初始值如果离实际值相差太大,在程序编写时,引入加速因子,加快其收敛速度。
Q:要使平方和最小,如果不能收敛怎么办?最后结果是局部最优解还是全局最优解?
A:收敛是一个逐步收敛过程,收敛是可以保证的,因为求的是距离,最后肯定能收敛;所得结果是一个局部最优解,但是不是全局最优解,实际数值计算过程验证了这点,但尚无法严格地从数学上证明该收敛点为全局最小值。